
と続いた「ワケがわからない」解説エントリも(多分)最後となります。
0.「スタック」という概念
スタック(stack)は、情報工学の分野でよく用いられるデータ構造の1つで、データを後入れ先出し(Last In, First Out; LIFO)の構造で保持するものです(wikipedia参照)。
……意味がわかりませんねw イメージがわきやすいようにすると、

こんな感じでしょうかw(この画像はココの商品ですね)
要するに、箱1つに何らかのデータが1つ入っていて、それらを積み重ねることで多数のデータの集合体を表す。で、データを追加するには積み重なった箱の一番上にデータ入りの箱を新たに置くしかない、データを取り出すのも一番上の箱からしか取り出せない、という感じです。
説明にいちいち写真使ってられませんので、イラストで描くことにしましょう。
図にあるように、追加したり取り出したりできる一番上の部分を「最上段」とか「トップ」「スタックトップ」といい、重なっている一番下の部分を「底」「スタックの底」といいます。またデータを格納している箱のことを「段」といったりします。
箱の中にどんなデータを入れることができるか、は実行環境依存で、『Glaeja』の場合は「実数のみ」となっています。
スタックが「箱が積み重なる」イメージだとすると、イラストでも上図のように箱を上に重ねていくべきなんでしょうが、それでは高くなりすぎて図示しにくいので、今後は下図のように横倒しにしたイメージで考えていきましょう。
横倒しに表記した場合、向かって左端が「底」、右端が「トップ」になります。
ちなみに、スタックに1つもデータがない(図でいうと1つも箱がない)状態のことを「スタックが空である」とか「空のスタック」といいます。
1.スタックの基本操作 ~プッシュとポップ~
では、このスタックにデータを追加したり取り出したりしてみましょう。
空のスタックに、最初に「2」を追加し、次に「7」を追加、最後に「0」を追加する様子を図に示すと、以下のようになります。
このようにスタックにデータを追加することを「プッシュする」とか「積む」とかいいます。プッシュは必ずスタック最上段におこなわれます。
では、上図スタックからデータを取り出してみましょう。データの取り出しはかならずスタック最上段からおこなわれます。
このようにデータをスタック最上段から取り出すことを「ポップする」といいます。
このとき、プッシュしたのとは逆の「0」→「7」→「2」の順にデータがポップされていることに注目してください。これが『後入れ先出し(Last In, First Out; LIFO)』ということです。
この『後入れ先出し(Last In, First Out; LIFO)』により、『スタックにプッシュしたデータは、ポップされるまで記憶される』という「スタック」の持つ重要な特徴がもたらされるわけです。
2.スタックを使った演算と後置記法
これで、プッシュとポップというスタックの基本操作が理解できたかと思います。では、なぜ「スタック」というデータ構造を使うのでしょうか。他のデータ構造ではダメなんでしょうか?
それは、スタックには他のデータ構造にはないいくつかの利点
- データ構造の実装が簡単
- スタックを使った「演算」ができる
- データを「後回し」にできる
3.の「後回し」にできる、というのは「データを記憶しておける」ということです。そして、この性質を利用することで、2.の「演算」をおこなうことができる、ということになります。
「演算」とは、まぁぶっちゃけ「計算」と同じような意味で、「ある法則に従って計算する」というものです。この演算の従う法則とか手順のことを「アルゴリズム」といいます。
コンピュータ内部でおこなわれる処理のほとんどは「演算である」ということができます。数値の加減乗除も「演算」ですし、数値同士の大小を比較するのも「演算」、ある物事が正しいか間違ってるか真偽を判断するのも「演算」です。
で、この「演算(ある法則に従って計算する)」がコンピュータ内部ではどのようなやり方(アルゴリズム)でおこなわれているのでしょうか。
例えば、「12+34」という演算をおこなう場合、兎にも角にも「12」と「34」という2つの数値をどこかに記憶しておかないといけません。また演算結果である「46」という数値も同様に記憶する必要があるでしょう。このようなものを記憶するのに「スタック」を利用しよう、というわけです。
やり方としては、「12」と「34」という2つの数値をスタックにプッシュして記憶しておいて、足すという演算をおこなうときには2つをポップして足し算してやり、その結果を代わりにスタックにプッシュして演算は終了です。
ちなみに、 上の例でいう「12」や「34」のような『演算されるもの』のことを「項」、「+」のような『どのような演算をおこなうか』を表す記号のことを「演算子」、「12+34」のように項と演算子で記述された演算全体のことを「式」といいます。
さて、データの記憶装置として「スタック」が利用できるとわかったので、実際に「12+34」という演算をおこなってみたいところなんですが、ここでちょっと面倒なことがあります。それは、「演算の前に『12+34』という文字列を解析して『「12」と「34」を足す』という意味を把握する」という文字列解析処理が必要なんですが、それが実に面倒くさいんですよね。
どう面倒くさいかというと、下図のような感じです。
『12+34』という文字列を解析すると、『「12」と「34」を足す』という意味を把握するのに、カーソル位置のマークして先読み、といった面倒くさい処理が必要になるわけです。…なんとかならんのでしょうか。この解析処理を簡単にするために、ちょっと人間側に苦労をしてもらいましょうw
『12+34』という文字列を『12 34 +』と書き換えてもらいましょう。途中の空白文字は2つの数値がくっついて「1234」という1つの数値と見間違えないための区切りです。
これの文字列解析は、上のものよりはるかに簡単になります。
この『12 34 +』のように演算子を項の後に書く記法のことを「後置記法(Postfix Notation)」といいます。また、ポーランド人論理学者ヤン・ウカシェヴィチが考案した「演算子を項の前に書く(+ 12 34)」ポーランド記法(Poland Notation)の逆なので「逆ポーランド記法(Reverse Poland Notation; RPN)」 ともいいます。これらに対し、普通の数式のような『12+34』という記法は「中置記法(Infix Notation)」といいます。
上図でもわかるように、この後置記法は非常にスタックと相性が良いので、スタックを使う演算はしばしばこの後置記法で記述されます。
この後置記法とスタックによる演算には、相性が良い以外に「カッコが不要」という便利さがあります。例えば、『2 3 4 + +』と後置記法で書かれた式は、以下のような順で演算されます。
これはよく見ると「3+4」を先におこなっているので、『2+(3+4)』というカッコ付きの式を演算したのと同じ順序になっていることがわかります。
では、『2 3 4 + *』と書かれた式はどうでしょう(乗算記号の「×」は英文字の"x"と見間違えないようアスタリスク"*"で表されます)。
この記述は『2*(3+4)』というカッコ付きの式を演算したのと同じ順序になるわかるかと思います。
ではカッコのない『2*3+4』(2*3を先に乗算し、それに4を加算する)は、どう記述すればいいのでしょうか。
簡単ですね、『2 3 * 4 +』と記述すればいいのです。
このように後置記法を用いることでカッコを用いることなく、カッコ付きと同じように演算順序を制御することが可能となるわけです。
…その分、演算順序をコンピュータに指示するために、記述順序を(人間が)調整してやらないといけませんので、一部の方々が力説するほど便利な記法だとは私個人は思いませんが…
3.スタックと関数
これで、加減乗除という四則演算をスタックによっておこなうやり方(後置記法に書きなおしてスタックを操作する)がわかったかと思います。では、ちょっと毛色の異なった演算について見てみましょう。
「関数」というものがあります。これは、平たくいうと「ある数を渡すと、ゴニョゴニョと処理をして、ある数を返してくれる」というものです。この関数も演算になります。
関数に渡す数のことを「引数」、関数から返される数のことを「返り値」といいます。
ある関数における引数の個数は、1個のこともありますし(例えば、ある数の正の平方根を返す関数)、 複数のこともあります(例えば、ある数AのB乗を返す関数は、A, Bという2つの引数を受け取る)。また、引数がゼロ個の場合もあります(例えば、「現在のバッテリー残量」を返す関数には引数は不要)。
同様に、ある関数が返す返り値の個数も、1個のこともありますし(例えば、ある数AのB乗を返す関数は AB という1つの返り値を返す)、複数のこともあります(例えば、ある数AとBの間にある整数全てを返す関数は[A, A+1, ..., B-1, B]という数の集合を返す)。また、返り値がゼロ個の関数もあります(例えば、スピーカー音量を50%にする関数は返り値を持つ必要がない)。
この関数というものをコンピュータ内に実現するにおいて、複数個の引数や返り値を記憶しておくためにもスタックが用いられます。
例えば、「ある数AのB乗を返す関数pow」というものを考えてみましょう。この関数に「2」と「3」を渡して「 23 」を返してもらいたい場合、馴染みのある記法ですと「pow(2, 3)」と記述しますし、後置記法ですと「2 3 pow」と記述します。この「2 3 pow」という記述が、スタックを使ってどのように演算されるのか見てみましょう。
…こんな感じですかね。呼び出し元が引数をスタックに積んで関数を呼び出し、呼び出された関数がそのスタックから引数を取り出して演算し、返り値をスタックに積んで呼び出し元へ返る、という一連の流れが理解できたでしょうか。
こうしてみると、スタックを用いて演算するにおいて、この「関数」と上で記した「(+や*等の)演算子」には本質的な違いがないことがわかります。以降では、面倒くさいので全てまとめて「演算子」と表記することにしましょうw
4.多様な演算子
さて、演算は、上で見てきたような「(いくつかの)数から、ある数を求める」というもの(数値演算)だけではありません。他にもいろんな種類の演算がありますので、ここではそのいくつかを見てみましょう。
例えば、「ある物事が、[A, B]という2つの状態のどちらに属するか分類する」という操作も演算にあたります。この2つの状態を「正しい(真)か」「正しくない(偽)か」と定めた場合、その結果(演算の返り値)のことを「真偽値(論理値、ブール値ともいう)」といいます。
このような「真偽値」を返す演算子というものを考える場合、スタックは真偽値を格納できるようになっていなければなりません。『Glaeja』を含む一部の環境におけるスタックでは数値しか格納できませんので、真偽値を数値で表現しなければなりません。そこで以降では、「偽」を「0」、真を「1(もしくはゼロ以外の数)」と定めておきます。
では、「渡された2つの数[A, B]について、AがBより小さい」という事柄について、それが正しい(真)か正しくないか(偽)かを返す関数(演算子)について考えてみましょう。このような「2つの項について大小等の関係性を比較する」演算子のことを「2項比較演算子」といいます。
「2つの数について、前者が後者より小さければ真、そうでなければ偽」を返す演算子を"<"と定義して、「2が3より小さければ真、そうでなければ偽」を後置記法で記述すると「2 3 <」となります。これをスタックで演算すると以下のようになります。
また、「真偽値を引数として渡されて、それらを演算した結果を真偽値として返す」演算子というものもあります(論理演算子)。
例えば、「2つの真偽値[A, B]について、それらが両方とも真であれば真、そうでなければ(どちらかが偽であれば)偽を返す」という2項論理演算子"and"を定義して、「2つの真偽値[真, 偽]について、"and"を演算」するときのスタックの様子は以下のようになります。
5.スタックによる演算の組み合わせ
上で見てきたように、スタックを用いた演算では、演算子による返り値も同じスタックに積まれ、記憶されます。ですので、ある演算の返り値を次の演算の引数とすること(上述した『2 3 * 4 +』)や、2つの演算結果を記憶しておいて後で別の演算の引数にすることも可能です。
後者の例として、「ある数Aが、2と5の間にあるなら真、間にない(2, 5に等しい場合も含む)なら偽」を返す演算を考えてみましょう。
まず、『2 A <』で「2がAより小さいなら真」という演算をおこないます。Aを「3」とすると、以下のような様子でしょうか。
こうすると(値が2つ積まれている)スタックの底には『2 A <』の結果が、最上段には『A 5 <』の結果が積まれていることになります。この2つを『and』で演算することで、「2と5の間にあるなら真、間にないなら偽」という演算がおこなわれました。
上記操作全てを後置記法で記述すると『2 A < A 5 < and』となります。
このように、スタックの持つ「データを記憶しておける」「データの演算ができる」という2つの性質を利用することで、複雑な演算をおこなうことが可能になっているわけです。
6.『Glaeja』におけるスタック演算の記述方法
さて、これで「スタックを用いた演算」を「後置記法」で記述する、ということが理解できたと思います。では、この「演算」を『Glaeja』でおこなわせるにはどうすればいいのでしょうか?
「テキスト」レイヤーの表示文字列に『2 3 +』と書いてみても、「5」と表示されるわけでもなく、式がそのまま「2 3 +」と表示されるばかりですw だって、『Glaeja』の文字列解析エンジンには「後置記法」を解釈してスタックを操作する機能がありませんからねw
ですので、『Glaeja』でスタックを用いた演算をおこなわせるには、上図で棒人間がおこなっている「スタックを操作する」ってのを、明示的に指示してやらなければなりません。
つまり『2+3』という演算をさせるには、まずスタックを用いた演算をさせるために『2 3 +』と後置記法に書き換えた上で、それをさらに『2@0/1/\p@3@0/1/\p@+@0/1/\x@』("2"をプッシュ、"3"をプッシュ、"+"を演算子とみなしてスタック演算)とスタック操作用の前方文字置換エスケープキャラクタに書き換えてやらなければなりません(「@0/-1/\p@」は「@p@」、「@0/-1/\x@」は「@x@」と糖衣構文を使って短縮できます)。
この後置記法からスタック操作用の前方文字置換エスケープキャラクタへの書き換えは、面倒ではありますが、数値なら「@p@」、演算子なら「@x@」を機械的に書き加えていくだけですので、特に難しいことはないでしょう。
例えば、上で示した『2 A < A 5 < and』は、"A"が"3"なら『2@p@3@p@<@x@3@p@5@p@<@x@and@x@』と書き換えられます。
結局のところ、難しいのは『やりたい演算を後置記法に書き換える』というところで、これはもう「慣れるしかない」としか言えませんw
7.スタック自体を操作する演算子
これまでに見てきた演算子は、全て「スタックからいくつか値をポップし、それらを演算して、結果をスタックにプッシュする」という共通の動作をおこなっています。例えば「+」ですと「スタックから2つ値をポップし、それらを加算して、結果をスタックにプッシュ」しています。
このように「演算子とはスタックをプッシュしたりポップしたりするものである」と考えると、「プッシュ」や「ポップ」自体も演算子の一種である、と見なせます。
ここでは、『Glaeja』に実装されている「プッシュ」「ポップ」以外のスタック自体を操作する演算子を見てみましょう。
・dup
「dup」は「duplicate(複製)」の略で、演算子の機能は「スタック最上段の値を複製してプッシュ」です。
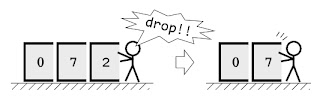
・drop
「drop」の機能は「スタック最上段の値を破棄」です。「ポップ」でも破棄はされるのですが、「drop」は表示がおこなわれません。
・rot
「rot」は「rotation(回転)」の略で、演算子の機能は「スタック底の値をポップして最上段へプッシュ」です。
・-rot
「-rot」は「rot」の逆の機能を持ち、「スタック最上段の値をポップして底へプッシュ」します。
・roll
「roll」の機能は、「スタックからポップした値を i とし、残ったスタックの最上段をゼロとする i 番目の値をスタック最上段へ移動」です。文章ではわかりにくいですが、下図のような操作をおこなうものです。
・dump
「dump」は、「現在のスタック全段の値を、底を先頭とするコンマ区切りの文字列として出力」します。出力は文字列解析エンジンの結果文字列に出力されます。これで「スタック」の解説はとりあえず終了です。




















0 件のコメント:
コメントを投稿